Computer Graphics

课程视频

学习新知识的方式：Why, What and How

Lecture3. Transformation

2D变换

  • 缩放矩阵(Scale)

  • 反射/对称矩阵(Reflection)
    以水平对称为例：

  • 切片矩阵(Shear)

  • 旋转变换(Rotate)

  • 逆变换(Inverse)
    求原先变换矩阵$M$的逆矩阵$M^{-1}$即可。

齐次坐标

  • 为什么要用齐次坐标？
    • 将各种变换进行统一，可以用统一的矩阵T表示变换矩阵
      增加一维：
  • 2D点：$(x, y, 1)^T$，or $(x, y, w)^T = (x/w, y/w, 1)$ 并且 $w!=0$
  • 2D向量：$(x, y, 0)^T$,
    • 向量加0是为了保护向量的平移不变性，同时可以区分向量与点，而且向量与点的计算结果类型也得到直观体现(1为点，0为向量)
  • 三维坐标同理

矩阵知识

  • 某矩阵的逆矩阵和转置矩阵相同，则该矩阵为正交矩阵

Lecture4. 观测变换(Viewing transformation)

视图变换(View/Model transformation)

简而言之是照相机(观察点)的位置

  • Position: $\hat{e}$
  • Look-at: $\hat{g}$
  • Up direction: $\hat{t}$

照相机摆放到原点，并将观察方向指向-Z，Up方向指向Y。

  • 先平移$\hat{e}$到原点
  • 旋转观察方向和up方向，直接秋旋转矩阵不好求，但是可以根据正交矩阵逆与转置相同的性质先求旋转的逆矩阵，即：

相机移动之后，模型也需要根据这些矩阵移动到相对应的位置，以保持和相机的相对位置不变。

投影变换(projection transformation)

正交投影(Orthographic projection)
透视投影(Perspective projection)

透视投影->正交投影，+正交投影就得到了透视投影

假设相机在原点，近景z坐标为n，远景z坐标为f。如何挤压远景得到和近景等大的正交投影的画面

  • 挤压后近景完全不变，而远景的x、y坐标与近景一致，z坐标不变。

根据相似三角形的对应关系得到最终挤压矩阵$M_{persp->ortho}$:

$ => M{persp->ortho}*M{persp} = M_{ortho}$

Lecture5/6. Rasterization(光栅化)/Antialiasing(反采样/抗锯齿)

光栅化：简而言之就是将图形空间里的models采样到二维图像里，并通过以希望物理设备进行展示，也就是现在的各类显示器。

锯齿：由于采样->光栅化这个过程中的最小单位是像素，是从连续到不连续，因此采样的结果与实际有区别，常常会形成锯齿。因此需要技术来解决这个问题，即抗锯齿。

由傅立叶变换可知，任意函数可以转换为许多不同频率的信号之和，因此对于不同频率的信号不能使用相同频率的采样方法，否则采样的结果会与实际差距太大。

走样：不同频率的函数的采样结果无法区分（说明采样频率有问题），因此出现走样。

  • 时域的卷积==频域的乘积
  • 高通滤波求边界，低通滤波模糊

反采样的方法

  • 增加采样率：像素小，采样率更高
    • 这是物理限制。
  • 采样前模糊(Pre-Filter)：没有改进判断单个像素颜色的方法，而是对图形进行模糊处理
    • 如何模糊：低通滤波器过滤掉高频波—>各种滤波器
    • 结果：效果还可以，先采样后模糊不行
  • 超采样：对单个像素进行多点采样，再将采样结果进行卷积（也就是平均/滤波），就可以实现更精准的模糊效果

z-buffer

  • 复杂度：O(n)，n是三角形的个数
  • 可能不只是对每个像素操作，而是对每个采样点操作，比如超采样
  • 处理不了透明物体，因为有$\alpha$

Shadow Mapping

单独的光栅化不考虑物体间的相互遮挡，然而这与实际不符，于是引入Shadow Mapping。但它还是存在走样现象的。

重要现象：阴影中的点只有视点能看到，但是光源看不到

过程：

  • 从光源（必须是点光源）看向场景，根据z-buffer的方式记录各点的深度值（以像素为单位，总体上也就是一次光栅化）
  • 从摄像机/眼睛看向场景，对看到的每个点，查看光源记录的深度。如果记录的深度与点的深度一致，则该点在阴影外；否则，在阴影内。

问题：

  • 只能做硬阴影（point light only），边缘非常锐利
  • 数值精度导致深度对比判断有问题
  • 光源的分辨率与视点的分辨率不同，又会导致计算的时候会出问题，比如光源分辨率太小就会使得一个像素记录太多信息，即出现了走样。

软阴影的存在就是因为光源存在大小，而每个顶点并不是都能看到所有光源，因此存在本影与半影的区别，也正是因此才有了软阴影。

Lecture7/8/9. Shading

Illumination & Shading

Blinn-Phong着色模型：ambient(环境光) + diffuse(漫反射) + specular(高光)
  • 1.基础定义：
    • 视点向量：v
    • 光源向量：l
    • 物体法线向量：n
  • 2.Lambert’s余弦定律：$cos\theta = l \cdot n$
  • 3.点光源的传播随距离增加而衰减，$r^2$级
  • 结合1/2/3 =>
    • 反射出去的值diffuse: $L_d = k_d(L_i/d^2)max(0, n \cdot l)$
    • $k_d$: 材料本身的漫反射系数，表示为(r,g,b)的三通道color值
    • $L_i$: 光的颜色
    • 与观察方向v无关，漫反射向各方向的反射相同
  • 4.关于高光的定义
    • 镜面反射方向向量: R
    • 半程向量: h ($h = \frac{v+l}{||v+l||}$)
  • 5.半程向量h与法线向量n是否接近
  • 结合4/5 =>
    • 镜面反射(高光)specular: $L_s = k_s(L_i/r^2)max(0, n \cdot h)^p$
    • $k_s$: 材料本身的漫反射系数，表示为(r,g,b)的三通道color值
    • $L_i$: 光的颜色
    • $p$: 因为实际高光区域很小，仅仅是余弦不足以表现真实的高光，一般在100~200
  • 环境光照ambient：$L_a = k_aI_a$
    • $k_a$: 材料本身的漫反射系数，表示为(r,g,b)的三通道color值
    • $L_a$: 光的颜色
    • 不考虑光线方向、观察方向、法线方向
    • 真正的全局光照非常复杂，这里是大胆假设，简化了模型
  • 结合ambient + diffuse + specular =>
    • $L = L_a + L_d + L_s$
Shading频率
  • Flat Shading: 每个三角面一个法线向量，面的颜色处理的一模一样
    • 效果较差
  • Gouraud shading
    • 求出所有顶点法线向量，计算出各顶点颜色值
      • 各面求和或加权求和，再归一化
    • 三角形内的点通过顶点颜色值作插值得到(即不用求法线向量)
  • Phong Shading：逐像素
    • 求出所有顶点法线向量，计算出各顶点颜色值
    • 三角形内的像素点的法线向量通过顶点法线向量作插值得到，再计算颜色值(即要求法线向量)
    • 逐像素着色

Grahics Pipeline(图形管线)

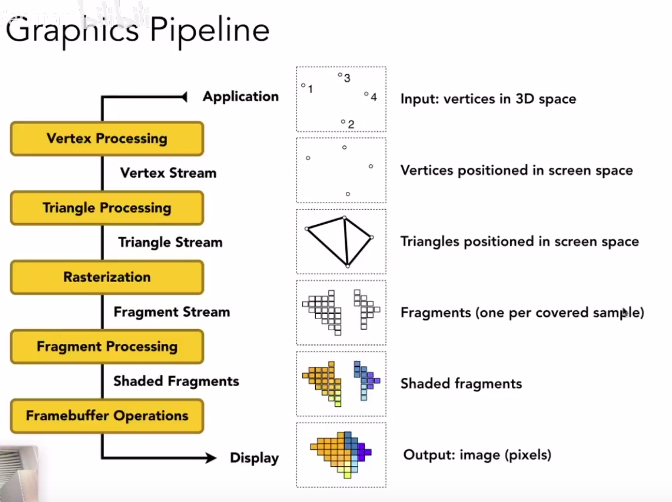
Graphics Pipeline

  • Vertex Shader: 顶点着色器
  • Fragment Shader: 像素/片段着色器

Texture Mapping(纹理映射)

  • 纹理放大：

    • 双线性插值
    • 双立方（三次）插值
      • 效果更好，开销更大

  • Mipmap

    • 快速的、近似的、方形的范围查询
    • 根据原纹理计算出更小分辨率的纹理
    • 计算level D的Mipmap:
      • $L = max(\sqrt{(\frac{du}{dx})^2 + (\frac{du}{dy})^2}, \sqrt{(\frac{dv}{dx})^2, (\frac{dv}{dy})^2})$
      • $D = log_2L$
    • 现在的查询是离散的，无法计算类似1.2层的结果。因此有三线性插值的方法，实现比较连续的插值结果
      • 1.在D层求插值
      • 2.在D+1层求插值
      • 3.求层与层的插值
  • Anisotropic Filter(各向异性过滤)
    • Mipmap只能处理正方形的纹理缩小，而各向异性过滤可以对不同的维度采取不同的缩小策略
      插值
  • 线性插值：$lerp(x, v_0, v_1) = v_0 + x(v_1-v_0)$
  • 双线性插值：
    • $u0 = lerp(s, u{00}, u_{10})$
    • $u1 = lerp(s, u{01}, u_{11})$
    • $f(x, y) = lerp(t, u_0, u_1)$

      重心坐标

  • 三角形内任一点$(x, y) = \alpha A + \beta B + \gamma C, \alpha+\beta+\gamma=1, \alpha >=0 \beta>=0, \gamma>=0$

  • 重心：$\alpha = \beta = \gamma = 1/3$

  • 结合重心坐标可以实现各种插值，颜色、纹理坐标、法线向量等等。

  • 三维空间中需要先计算插值再投影
  • 投影之后没有不变性，这是缺点

纹理应用

  • Environment Map(环境映射): 记录环境中各种光照信息
    • sphere map
    • cube map：将sphere map的内容映射到cube上
  • 凹凸映射(Bump mapping)
    • 并没有改变任何实际的几何信息，而是通过增加高度来计算新的法线向量，从而改变最终的着色。即：height->normal->shading
    • 纹理图中对u求导得：$dp/du = (\Delta u, 0, h(u+1)-h(u))$
    • 纹理图中对v求导得：$dp/dv = (\Delta v, 0, h(v+1)-h(v))$
    • 最终法线是两者叉积得到的结果，当然得注意方向：$normal = dp/du \cdot dp/dv = (-dp/du, -dp/dv, 1)$
  • 位移贴图(Displacment Mapping)
    • 也是存了高度，但是真的改了顶点位置
    • 模型更细致更好，能更好的表现贴图结果

Lecture10/11/12. Geometry

  • 分类：隐式几何，显式几何
    • 结合需要进行选择
  • 隐式几何：
    • 不给实际的点，用隐函数表示点坐标的关系，比如$x^2+y^2+z^2=1$
    • 具体解释该几何体是什么很复杂，但是判断单个点的内外位置很容易
  • 显式几何：
    • 直接给出所有点坐标，或者用参数映射
      • 参数映射：
        • 遍历(u, v)就能得到所有点的集合
        • 例：$f(u, v) = ((2+cosu)cosv, (2+cosu)sinv, sinu)$
    • 判断内外位置很复杂，判断形状比较简单

隐式表现方法

  • CSG
    • Constructive Solid Geometry: 将简单的基本几何组合起来得到复杂的几何
  • Signed Distance Function(符号距离函数)
  • Level Set(水平集)
  • Fractal(分形)

显式表现方法

  • 点云
  • 多边形网格
  • 贝塞尔曲线(通过参数t定义)

    贝塞尔曲线

    用一系列的控制点$p_0…p_n$去定义某个曲线。

曲线一定经过$p0$和$p_n$，且在$p_0$和$p_n$的切线与$p_0$,$p_1$和$p{n-1}$，$p_n$的切线相同

  • 画线的算法：

    • 假设$p_0$是时间0的点，$p_n$是时间1的点，需要找出时间t(t<1)的点在哪。遍历就能画出曲线上的所有点
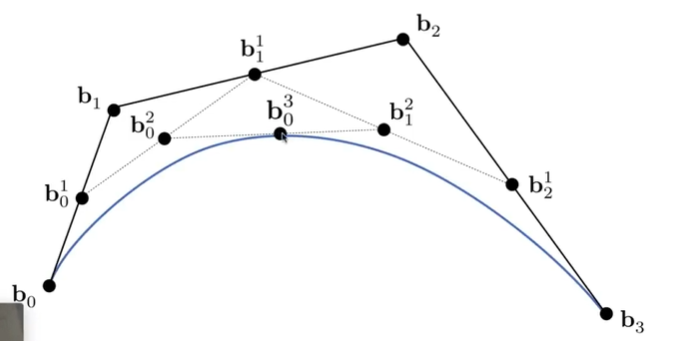
    • 推导过程见下图，就是一个递归求t的过程 bezier t
    • 总结公式：(n+1)个控制点$p0…p_n$，公式就是$b^n(t)=b_0^n(t) = \sum{j=0}^nb_jB_j^n(t)$，$B_j^n(t)$就是多项展开式的值
      • $B_i^n(t) = \left( \begin{matrix} n \ i \end{matrix} \right) t^i (1-t)^{n-i}$

  • 仿射变换下贝塞尔曲线是一致的。先变换后画线/先画线后变换是一样的，因此可以只存控制点，做变换之后再画出来，不用记录所有点。

  • 投影变换下不适用。
  • 凸包性质：不会超过给定控制点形成的凸包范围
逐段贝塞尔曲线

复杂曲线由多段简单贝赛尔曲线组成，一般这些简单贝赛尔曲线都是用4个控制点。

  • 连续性：
    • c0连续：曲线A的终点就是曲线B的起点
    • c1连续：c0连续，且该重合点切线相同
B-splines(B样条曲线)

比贝塞尔曲线更好，修改的时候只有局部会发生改变

贝塞尔曲面

简单来说就是现在u方向上的时间t1上得到n条贝塞尔曲线，然后再对v方向上的时间t2的n个点再求一次贝塞尔曲线的点。

因此这里需要两个参数$t_1$，$t_2$

Mesh Operations(网格操作)

Mesh Subvision(网格细分)(UpSampling)

  • Loop细分
    • 将一个三角形分成4个（各边中点相连）
    • 对各新旧顶点进行不同的顶点位置更新
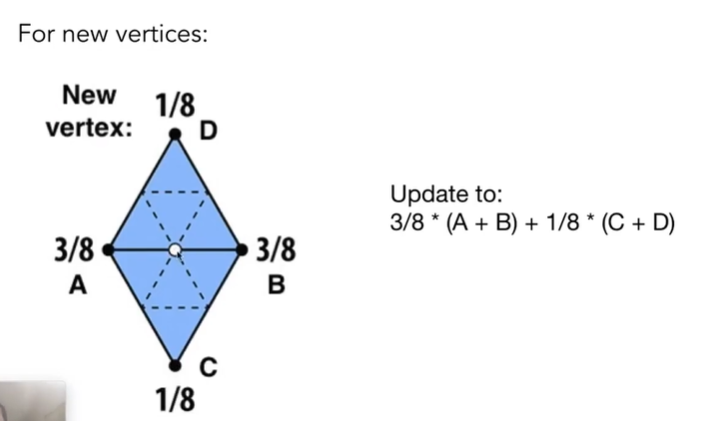
      • 对新顶点的更新方式：（白点） new vertex
      • 对旧顶点的更新方式：（白点）
        • n: 该顶点的度
        • u: 考虑周围顶点的值
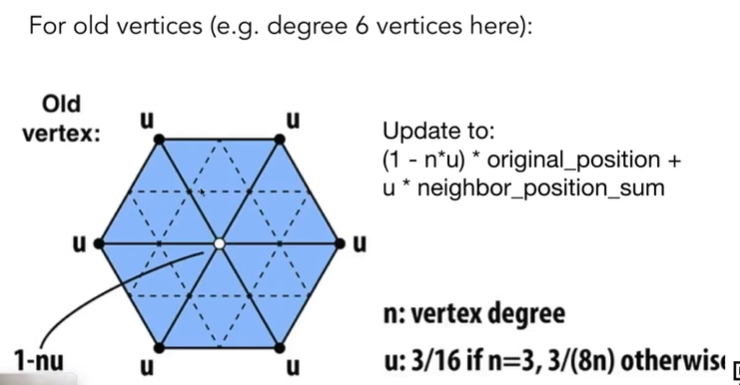
        • old vertex
    • 只能用三角形面
  • Catmull-Clark细分
    • 基础定义：
      • quad face: 四边形的面，non-quad face: 非四边形的面
      • Extraordinary vertex: 奇异点，度不为4的点
    • 取各边和各面的中点，并且面中点与边中点连接
    • 一次细分之后，non-quad面都变成了quad面，代价是多了一个奇异点。因此之后无论再做几次，奇异点都不会再增加，因为non-quad面在第一次就没了。
    • 点的更新
      • 面的中心点由四边顶点决定，边中点的规则和旧顶点的规则均如下：
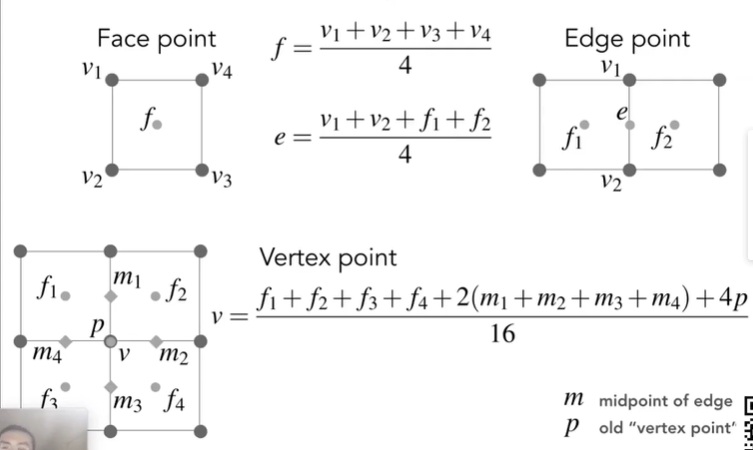
      • Catmull Clark

Mesh Simplification(网格简化)(DownSampling)

  • Collapse Edge：一条边坍缩成一个点
    • Quadric Error Metrics(二次误差度量)：新的点到与原来的边有关的面的距离的平方和最小，就是该边最优的坍缩位置
      • 问题：某边的坍缩会影响相邻边的二次误差度量值 => 用最小堆，取最小值，更新受影响的值，更新堆，再取最小值
      • 这其实是贪心算法，没法全局取坍缩的边

Mesh Regularization(网格正则化)(Same #Triangles)

Lecture13/14/15/16. Ray Tracing

光线追踪需要解决的问题：

  • 软阴影(Soft shadows)
  • Glossy reflection(类似铜镜这种有反射但是不是纯反射还有自身材质的东西)
  • 间接光照(Indirect illumination): 类似于环境光的真实模拟

光线追踪类型：

  • Pinhole Ray Tracing
  • Recursive(Whitted-style) Ray Tracing
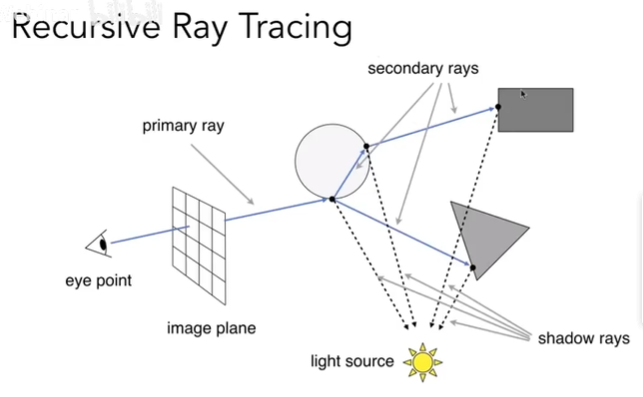
    recurcive ray tracing

光线追踪的技术问题

  • 光线与物体表面的焦点

    • 光线：$r(t) = oringin + t * direction, 0 \le t < \infty$
    • 与隐式表面的相交计算，假设隐式函数为$f(p) = 0$，有$f(origin+t*direction) = 0$，需要的解是正数解
    • 与显式表面相交计算，
      • 也就是与三角形求交点 <=> 光线与三角形所在平面求交 + 交点是否在三角形内。交点p，$(p-p’) \cdot N = (origin + t * direction - p’) \cdot N = 0 => t = \frac{p’\cdot N-origin}{direction \cdot N}$，检查：$0 \le t < \infty$
      • Moller Trumbore算法：
        • 光线上的点与三角形上的点相交有: $origin + t*direction = (1-b_1-b_2)p_0 + b_1p_1+b_2p_2$，最终结果如下：
          $\left[ \begin{matrix} t \ b_1 \ b_2 \end{matrix} \right] = \frac{1}{S_1 \cdot E_1} \left[ \begin{matrix} S_2 \cdot E_2 \ S_1 \cdot S \ S_2 \cdot D \end{matrix} \right]， \begin{matrix} E_1 = p_1 - p_0 \ E_2 = p_2 - p_0 \ S = O-p_0 \ S_1=D \times E_2 \ S_2=S \times E_1 \end{matrix}, 检查: \begin{matrix} 0 \le t < \infty \ 0 \le b_1 \le 1 \ 0 \le b_2 \le 1 \ \end{matrix}$

  • 加速光线与表面求交的加速(显然不能与每个三角形都求一次)

    • Bounding Volumn(包围盒): 用简单的三维物体包围复杂的三维物体，那么计算相交时就需要先和简单物体作相交判断，不相交则直接pass，节省了大量计算量。
      • Axis-Aligned Bounding Box(AABB): 轴对齐包围盒，这个常用。与这个包围盒的相交判断算法十分简单，这里不做记录了。
    • Uniform Spatial Partitions(Grids): 不适用于大规模的空白，如果空间中只有某一小块有物体，那格子会非常小，这样按步判断计算量反而很大
    • 空间划分：
      划分的停止条件，某块为空或者块内的物体数量足够少
      • Oct Tree: 八叉树
      • KD Tree: 与八叉树类似，但是递归切分时一次只切分为两块；为了切分均匀，轴向的切分需要有顺序，例：x->y->z->x->y->z…
        • 并不是按物体划分，因此后续的物体判断比较复杂
      • BSP Tree: 不是横平竖直，随着维度增加，切分计算越来越复杂，不如KD Tree.
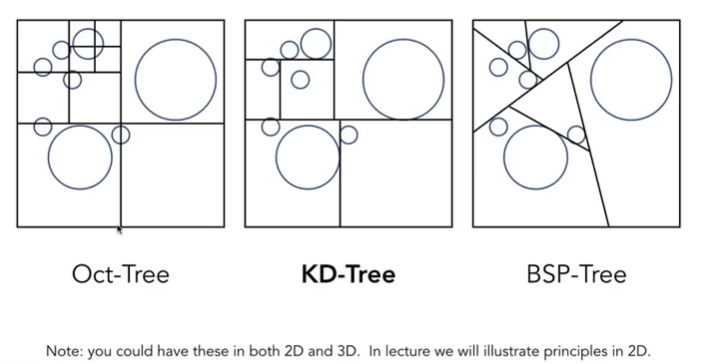
        spatial partition
    • Bounding Volume Hierachy(BVH): 以空间物体划分，生成类似KD Tree的树，空间上可能重叠，终止条件是盒子里物体足够少。
      • 问题：空间上不是严格分开，因此如何划分以减少重叠空间就是值得研究的问题

Basic radiometry(辐射度量学)

物理上准确定义光线的方法。

基础定义：

  • Radiant Energy: 电磁辐射的能量，以焦耳为单位$Q [J = Joule]$
  • Radiant flux: 单位时间的能量（功率），以瓦特为单位$\Phi = \frac{dQ}{dt}[W = Watt][lm=lumen]^*$，图形学更多用的是功率
  • Radiant Intensity: 单位立体角辐射出去的能量，$I(w) = \frac{d\Phi}{dw}[\frac{W}{sr}][\frac{lm}{sr} = cd = candela]$
    • 立体角=面积/半径的平方：$\Omega = \frac{A}{r^2}$
  • Irradiance：
    • 接受辐射，或者是光源往外辐射
    • $E(x) = \frac{d(\Phi)}{dA}$
    • 联系Lambert’s Cosine Law，因为有这个定义，才有那个法则
    • 也能解释季节变化，因为自转导致直射纬度在变

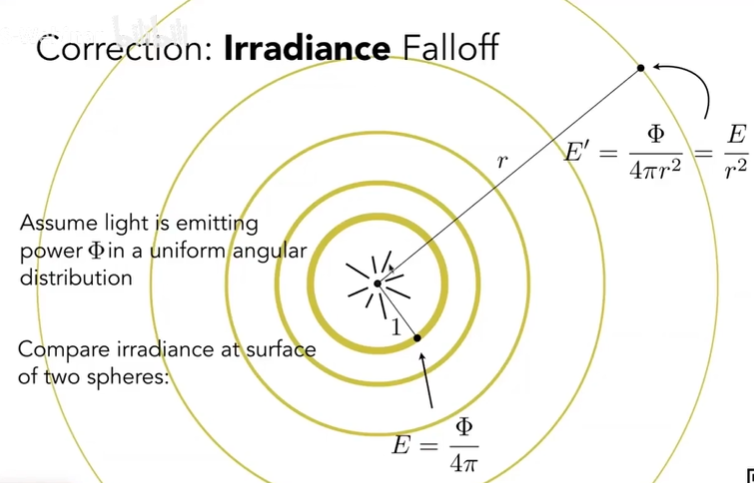
    • Irradiance衰减图示
  • radiance：
    • 单位立体角、单位辐射面积上的功率
    • $L(p, w) = \frac{d^2\Phi(p, w)}{d\omega dA cos\theta}$，$cos\theta$是irradiance的夹角

BRDF

BRDF：Bidirectional Reflection Ditribution Function双向反射分布函数，描述一束入射光的反射光的分布

  • BRDF：某个入射方向的出射方向的贡献分布计算式

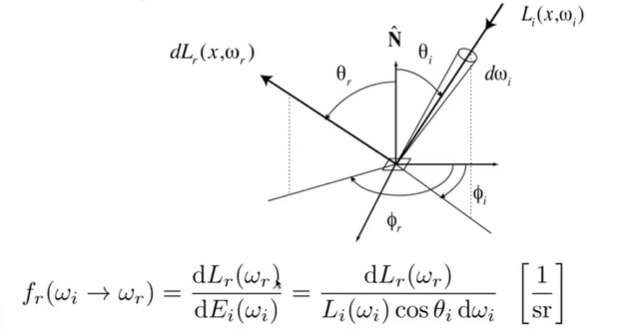
    BRDF: 入射光与反射光
  • 反射方程(光线计算)：某个出射方向的光线计算式（即各个反射量的求和/积分）
    • $Lr(p, \omega_r) = \int{H^2}f_r(p, \omega_i \rightarrow \omega_r)L_i(p, \omega_i)cos\theta_i d{\omega}_i$
  • 渲染方程：
    • 反射光 = 自己发光+反射别人的光
    • $Lo(p,\omega_o) = L_e(p, \omega_o) + \int{\Omega^+}L_i(p,\omega_i)f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) d{\omega}_i$，其中$n \cdot\omega_i = cos\theta_i$
    • 方程简化
      • 最终算式：$L = E + KE+K^2E+ K^3E+…$
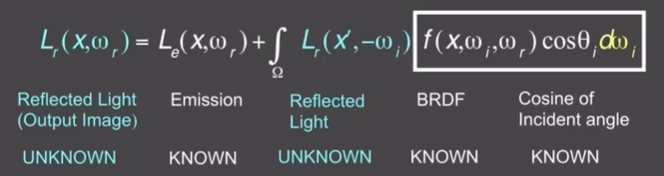
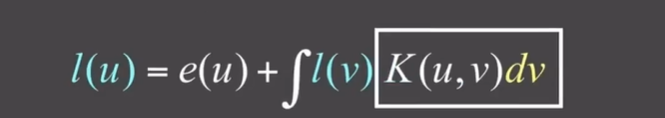
        original ./simmplify
    • 光栅化只能做到$E$和$E+KE$

Monte Carlo Intergration(蒙特卡洛积分)

求解难以计算解析解的函数的定积分：$\int_a^b f(x)dx$

  • 常规算式：$\int f(x)dx = \frac{1}{N} \sum_{i=1}^{N} \frac{f(X_i)}{p(X_i)}$，$X_i$ ~ $p(x)$，$N$越大越准确

解渲染方程

  • Simple蒙特卡洛解法(不考虑自光源)
    • 直接光照下
      $Lo(a,\omega_o)
      =\int      {\Omega^+}Li(a,\omega_i)f_r(a, \omega_i, \omega_o) (n \cdot \omega_i) d{\omega}_i
      =\frac{1}{N} \sum      {i=1}^{N} \frac{L_i(a,\omega_i)f_r(a, \omega_i, \omega_o) (n \cdot \omega_i)}{p(\omega_i)}$
  • 考虑物体发光，也就是考虑间接反射。
    • 只要假设某点也会从其他点接受光线，那么它本身就像是摄像机，于是就形成了递归，递归伪代码如下：

      蒙特卡洛方法——N
  • 每条入射光产生N条出射光的结果会导致光线数量爆炸。因此上述伪代码无法实现。解决办法也很简单，每次只产生一条，然后在该点随机N次，取N次结果的平均以得到噪声较小的结果。代码如下：

    蒙特卡洛方法——1

    Ray Generation

  • 解决无限递归：采用概率p决定是否往下递归。伪代码如下：


    解决无限递归

  • 在着色点上采样，光的传播结果大部分都是一种浪费。因此我们将对着色点采样改为对光源采样，这样可以节省大量无用的计算量

    • 首先是立体角到光源面积的积分转换，关系：$d\omega_i = \frac{cos\theta’}{||x’-p||^2} dA$，$\theta’$是光源面的法线向量与入射光线的夹角，$||x’-p||^2$光源点到入射点的距离的平方(这个不难理解)
    • 得到新的渲染方程：$Lo(a,\omega_o)
      =\int      {\Omega^+}L_i(a,\omega_i)f_r(a, \omega_i, \omega_o) (n \cdot \omega_i) \frac{cos\theta’}{||x’-p||^2} dA$
    • 因此，可以对光源进行简单的均匀采样(即概率为常数)，然后计算贡献度和，取平均。
    • 注意，有物体遮挡的时候也要考虑进去，这是直接光照和间接光照（其实也就是变相的直接光照）都要考虑的。
    • 伪代码如下：

      光源采样

Lecture17. Materials and Appearances(材质外观)

  • Diffuse / Lambertian Material
    • BRDF $f_r = \frac{\rho}{\pi}$，其中$\rho$是albedo，既可以是材质的颜色，也可以是纹理，参照unity里的设置
  • Glossy Material(抛光金属)
  • Ideal reflective / refractive material (BSDF*)
    • 水、玻璃等既可反射也可折射的材质(也有部分吸收)
    • 折射定律：Snell’s Law
      • $\eta_i sin\theta_i = \eta_t sin\theta_t$
  • Specular
  • Fresnel Term(菲涅尔项，$\eta = 1.5$)
    • 视线方向与法线方向越接近平行，折射就越是严重；反之，反射就越严重。
    • Schlick’s近似算法：$R(\theta) = R_0 + (1-R_0)(1-cos\theta)^5$，其中$R_0 = (\frac{n_1 - n_2}{n_1 + n_2})^2$，$n_1,n_2$就是两种介质的折射率。
  • Microfacet Material(微表面材料，非常重要！！！)
    • 从近处看能看到微表面的细节，能看到凹凸不平的、但是能出现镜面反射的；从远处看能看到平坦粗糙的外观。
    • 近处是几何，远处的材质
    • 因此，微表面上法线方向不同但大体相同也就是Glossy的材质
    • $f(i,o) = \frac{F(i, h) G(i,o,h) D(h) }{4(n,i)(n,o)}$
      • F(i, h)：$F{Schlick} = C{spec} + (1-C{spec})(1-l \cdot h)^5$(考虑了高光颜色$C{spec}$)，菲涅尔项，描述光的反射与折射量
      • G(i,o,h)：$G_{Cook-Torrance} = min(1, \frac{2(n \cdot h)(n \cdot v)}{v \cdot h}, \frac{2(n \cdot h)(n \cdot l)}{v \cdot h})$ shadow-masking项，可以处理边界处太亮的情况
      • D(h)：$D_{GGX} = \frac{\alpha^2}{\pi ((n \cdot h)^2(\alpha^2-1)+1)^2}$，法线分布

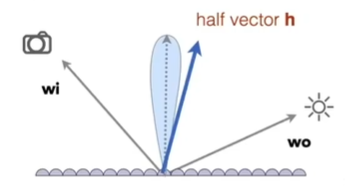
        微表面模型
  • Isotropic / Anisotropic Materials(各向同性/各向异性材料)
    • 与绝对方位角有关

Lecture18. Advanced Topics in Rendering

  • 无偏：unbiased，利用蒙特卡洛方法计算的估计的期望和实际的相等的。(也就是概率上的无偏性)
  • 有偏：biased，与unbiased相反。
    • 一致：consistent，原本有偏，收敛之后是无偏的。

无偏光线传播算法

  • BDPT: Bidrectional Path Tracing
    • 从光源和视点同时采样得到半路径，然后连接两个顶点得到整个路径。
    • 很难实现，速度也很慢，对某些情况的效果很好。
  • MLT: Metropolis Light Transport
    • 马尔科夫链的应用：蒙特卡洛积分法中，当采样分布与原函数基本一致的时候得到的误差是最小的。而马尔科夫链就可以生成这种与原函数基本一致的pdf。它可以生成与给定路径相似的路径
    • 复杂光路上效果很好。但是很难判断是否收敛

有偏光线传播算法

  • Photon Mapping
    • 能很好的处理Specular-Diffuse-Specular(SDS)和产生caustics
      • caustics: 由于光线聚焦产生的非常强烈的图案
    • 实现过程
      • stage 1: 从光源发散出photons，不断反射、折射它们，直到达到diffuse的表面。
      • stage 2: 从照相机发散出photons，不断反射、折射它们，直到达到diffuse的表面。
      • 计算：local density estimation
        • 对每个着色点，取其周围的N个photon，求出它们所占的面积，就能求出密度。密度越大的就应该越亮。
        • N越小的时候，noise就会比较大
  • Vertex Connection and Merging
    • BDPT和Photon Mapping的组合
  • Instant Radiosity(IR)实时辐射度
    • 不能处理Glossy的物体

Lecture19. Cameras, Lenses and Light Fields

Lecture20. Color and Perception

上述两讲内容与基本图形学关系不大，具体可以去看视频内容，这里不做记录。

Lecture21/22. Animation

  • 关键帧动画
  • 质点弹簧系统
  • 粒子系统
  • Forward Kinematics
  • Rigging(绑定)

Euler方法

  • 一阶(前向)欧拉方法
    • $x^{t+ \Delta t} = x^t + \Delta t x’^t, x’^{t+ \Delta t} = x’^t + \Delta t x’’^t$
    • 受步长$\Delta t$的影响误差可能很大，当然减小$\Delta t$可以减小误差
    • 非常不稳定，可能会出现不符合实际规律得到结果
  • 中点法（Midpoint method）
    • $x{mid} = x^t + \Delta t /2 \cdot x’^t \rightarrow x^{t+\Delta t} = x^t + \Delta t \cdot x’{mid}$
    • 上式化简得$x^{t+ \Delta t} = x^t + \Delta t x’^t + \frac{(\Delta t)^2}{2} x’’^t$
  • Implicit Euler Method
    • 与显式欧拉方法不同，隐式欧拉方法是用下一时刻的速度和加速度等量
    • $x^{t+ \Delta t} = x^t + \Delta t x’^{t+ \Delta t}, x’^{t+ \Delta t} = x’^t + \Delta t x’’^{t+ \Delta t}$
  • Runge Kutta Method
    • RK4,4阶，最常用
    • 假设初始条件$\frac{dy}{dt} = f(x, y), y(t_0) = y_0$
    • 有$y{n+1} = y_n + \frac{1}{6}h(k_1+2k_2+2k_3+k_4), t{n+1} = t_n + h$
    • 上式中$k_{1-4}$的值如下：$\left[ \begin{matrix} k_1 \ k_2 \ k_3 \ k_4 \end{matrix} \right] = \left[ \begin{matrix} f(t_n, y_n) \ f(t_n+\frac{h}{2}, y_n+h \frac{k_1}{2}) \ f(t_n+\frac{h}{2}, y_n+h \frac{k_2}{2}) \ f(t_n+h, y_n+hk_3) \end{matrix} \right]$
  • Position Based / Verlet Integration

大规模粒子的模拟方法

  • 拉格朗日法（质点法）
    • 对每个单独的粒子计算其运动变化规律
  • 欧拉法（网格法）
    • 划分空间，以空间为单位考虑
  • Material Point Method(MPM)
    • 现在非常热门的方法，也是拉格朗日法和的结合